Большая Советская Энциклопедия
(БСЭ)
|
|
|
|
источник статьи: Большая Советская Энциклопедия (БСЭ) |
|
Возможных перемещений принцип, один из вариационных принципов механики, устанавливающий общее условие равновесия механической системы. Согласно В. п. п., для равновесия механической системы с идеальными связями (см. Связи механические) необходимо и достаточно, чтобы сумма работ dAi, всех приложенных к системе активных сил на любом возможном перемещении системы была равна нулю. Математически В. п. п. выражается уравнением где Fi — действующие активные силы, dsi — величины возможных перемещений точек приложения этих сил, αi — углы между направлениями сил и возможных перемещений. Для систем с несколькими степенями свободы уравнение (1) должно составляться для каждого независимого перемещения в отдельности. Таким образом, В. п. п. позволяет найти условия равновесия системы, не вводя неизвестных реакций связей, что существенно упрощает решение и расширяет класс разрешимых задач. Например, с помощью В. п. п. легко найти условия равновесия подъёмного механизма, детали которого скрыты в коробке К (см. рис.). Из уравнения (1) получаем где Р и Q — действующие силы. Для окончательного расчёта надо установить зависимость между перемещениями dsB и dsD. Если при одном повороте рукоятки АВ винт поднимается на величину h, то эта зависимость найдётся из пропорции dsB: dsD = 2pa: h, где а — длина рукоятки. Окончательно уравнение (2) даёт следующее условие равновесия Р = Qh/2pa. Методами геометрической статики (если скрытые в коробке детали механизма неизвестны) эта задача вообще решена быть не может. О применении аналогичного метода к решению задач динамики см. Д'Аламбера — Лагранжа принцип. С. М. Тарг. 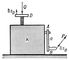 Рисунок к ст. Возможных перемещений принцип. |