Большая Советская
Энциклопедия
|
|
|
|
источник статьи: Большая Советская Энциклопедия |
|
Пластичности теория, раздел механики, в котором изучаются деформации твёрдых тел за пределами упругости. П. т. изучает макроскопические свойства пластических тел и непосредственно не связана с физическим объяснением свойств пластичности. П. т. занимается методами определения распределения напряжений и деформаций в пластически деформируемых телах. Для определения пластических свойств металлов производятся эксперименты по растяжению — сжатию плоского или цилиндрического образца и деформированию тонкостенной цилиндрической трубки, находящейся под действием растягивающей силы, крутящего момента и внутреннего давления, т. е. эксперименты, позволяющие вести независимый отсчёт усилий и деформаций. Диаграмма зависимости «напряжение — деформация» (рис. 1) характеризует деформацию данного материала. П. т. идеализирует поведение реальных материалов при пластическом дефо рмировании, пользуясь различными гипотезами. Обычно в П. т. диаграмму «напряжение — деформация» апроксимируют схемой (рис. 2), состоящей из двух участков: отрезка прямой OA, соответствующего упругому состоянию материала, и отрезка AC, соответствующего состоянию пластичности. При пластическом деформировании напряженное и деформированное состояния материала существенно зависят от истории нагружения. Так, вторичное нагружение образца (после его разгрузки — прямая PM, рис. 1) повышает предел упругости материала (точка М вместо точки А) — т. н. упрочнение или наклёп. Поэтому данному напряжённому состоянию могут соответствовать различные пластические деформации в зависимости от того, какой последовательностью напряжённых состояний оно достигнуто. Определение модели пластического тела состоит в установлении связи между тензорами, определяющими сложное напряжённое и деформированное состояния материалов. Одной из наиболее распростр анённых является теория малых упругопластических деформаций (деформационная теория), которая формулирует соотношения между интенсивностью напряжений и интенсивностью деформаций в той же точке где sx, sy, sz — нормальные напряжения в координатных площадках, проходящих через данную точку, txy, tyz, tzx — касательные напряжения, ex, ey, ez — дефор мации удлинения, gxy, gyz, gzx — деформации сдвига. Для случая, когда интенсивность деформаций в данной точке возрастает, принимается, что величины si и ei связаны между собой независимо от вида напряжённого состояния. Деформационная П. т., строго говоря, применима лишь в случае простого нагружения, когда все компоненты напряжённого состояния возрастают пропорционально одному параметру. Более общей является теория течения, связывающая приращения деформаций и напряжении с компонентами напряжений. П. т. играет большую роль в технике, т.к. тесно связана с важнейшими вопросами проектирования конструкций, исследованием технологических процессов пластического деформирования металлов и т. и. Важные приложения П. т. относятся и к теории устойчивости пластинок и оболочек.
Лит.: Ильюшин А. А., Пластичность, Основы общей математической теории, М., 1963; Ишлинский А. Ю., Пластичность, в кн.: Механика в СССР за 30 лет, М.—Л., 1950; Качанов Л. М., Основы теории пластичности, М., 1956; Надаи А., Пластичность и разрушение твёрдых тел, пер. с англ., М., 1954; Прагер В., Ходж Ф. Г., Теория идеально пластических тел, пер. с англ., М., 1956. А. С. Вольмир.  Рис. 1. Диаграмма зависимости «напряжение — деформация» (s — e) для образца из мягкой малоуглеродистой стали: OA — упругая деформация; точка А — предел упругости (точнее — предел пропорциональности); В — предел текучести; BC — площадка текучести; MP — прямая разгрузки. 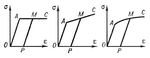 Рис. 2. Идеализированные схемы зависимости (s — e): а — идеально-пластический материал; б — материал с линейным упрочнением; в — материал с нелинейным упрочнением. |