Первый интеграл системы обыкновенных дифференциальных уравнений

  , i = 1, …, n

  — соотношение вида

(где С — произвольная постоянная), левая часть которого сохраняет постоянное значение при подстановке любого решения y₁ = y₁(x),..., y_n= y_n (x) системы, но не является тождественной постоянной (см. Дифференциальные уравнения). Геометрически П. и. представляет собой семейство гиперповерхностей в (n + 1)-мерном пространстве Oxy₁... y_n, на каждой из которых расположено некоторое подсемейство интегральных кривых системы. Например, одним из П. и. системы ,  является y² + x² = C² (круговые цилиндры); интегральные кривые у = Csin (x — x₀), z = Ccos (x—x₀) суть винтовые линии, расположенные на этих цилиндрах (см. рис.). Если известно k независимых П. и. Ф_i (x₁, y₁,..., у_п) = C_i (i = 1,..., k; k < n) системы, то её порядок, вообще говоря, может быть понижен на k единиц; если k = n, то общий интеграл системы получается без интегрирования.

  Лит.: Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959.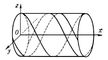

Рис. к ст. Первый интеграл.